疑似乱数
乱数 Random Numbers MathWorld
複雑系 Complex Systems MathWorld

バンダイナムコスタジオ 加来量一 4Gamer
またシミュレーションを行う上では、再現性のある乱数というのも求められるので、完全な乱数よりも逆に疑似乱数の方が良い場合もあります。

シードは乱数生成アルゴリズムの開始点として使用される初期値です。

ハードウェア乱数生成器 Wikipedia

プレシジョンダイスは、確率を1/6に近づけるために様々な工夫がなされている特殊なダイスです。普通のダイスですと各面に穴を掘っているため、重さに偏りがでてしまいます。プレシジョンダイスはそれを防ぐために同じ重さの樹脂で穴を埋めています。また、頂点の面取りをしているので、角が不均等に削れていくこともありません。透明になっており、おもりが入っていないことも一目瞭然です。
Precision Dice JBS

メーカーは世界で唯一の真性乱数発生器であることを語っている。この量子乱数発生器の動作原理はシンプルなものである。ボード内に用意された半透明の鏡に光量子(フォトン)を一つずつ照射し、反射するのか透過するのかという排反事象を観測することによって0および1のビット値に関連づける。このようにして生成されたランダムビットストリームを出力することによって真正乱数列として取り出すことができるようになる。
QUANTIS型は量子が本質的にランダムであるという原則に基づく真の乱数発生器です。
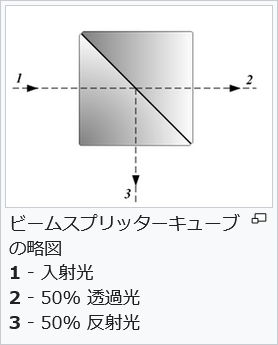
ビームスプリッター Beam Splitter Google Wikipedia Wikipedia

放射性物質を用いて量子乱数を生成してしまう猛者が現れる - GIGAZINE
Nathan Griffith GitHub
「無限に都市が生成されるアルゴリズム」で生成された都市を自由に歩き回ってみた - GIGAZINE
(「観測」によって)ある1つの固有状態に収縮すること
WaveFunctionCollapse GitHub Blog



セルオートマトン Cellular automaton Forvo コトバンク Wikipedia Wikipedia
Elementary Cellular Automaton Forvo Яндекс Google Wikipedia
Maze Generation algorithm Wikipedia
状態遷移図 State Diagram Wikipedia MathWorld
マルコフ連鎖 Markov Chain Forvo Wikipedia MathWorld
全域木 Spanning Tree Wikipedia Wikipedia MathWorld
End-to-End Wikipedia
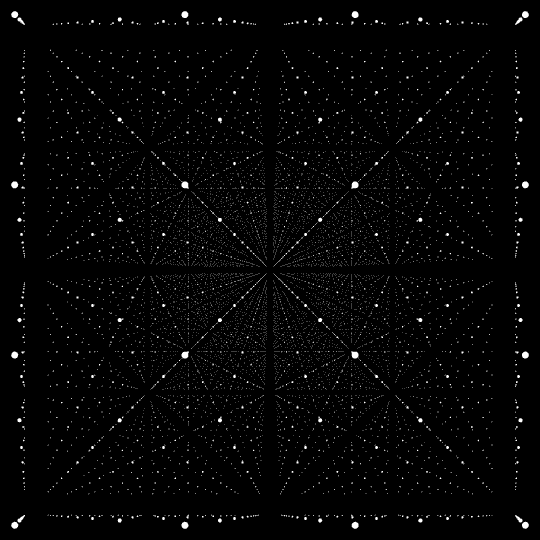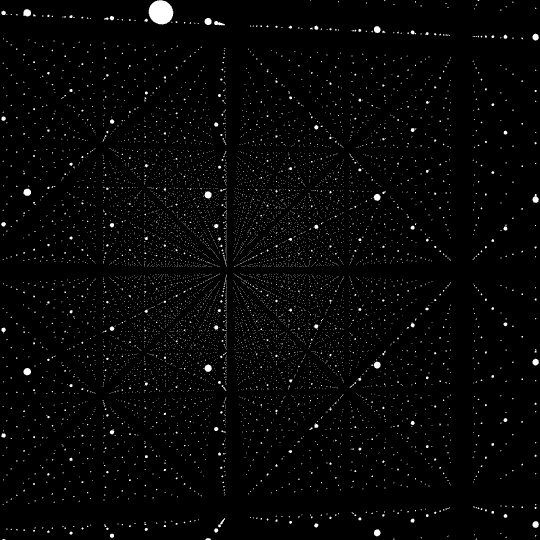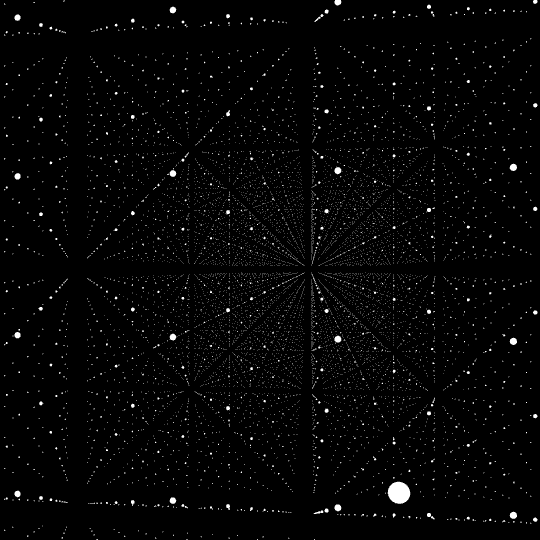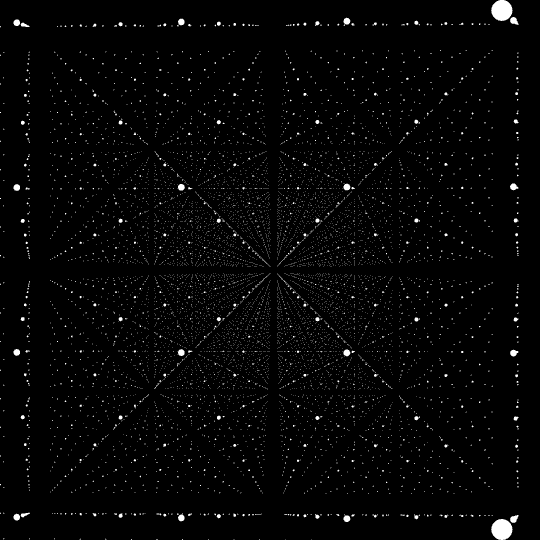
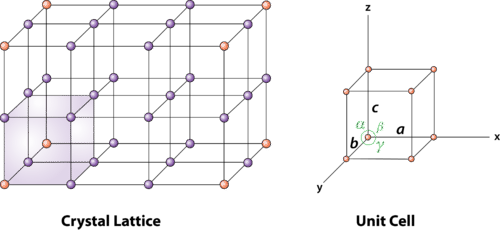
結晶構造 Crystal structure Wikipedia Wikipedia
単位格子 Unit cell Wikipedia Site
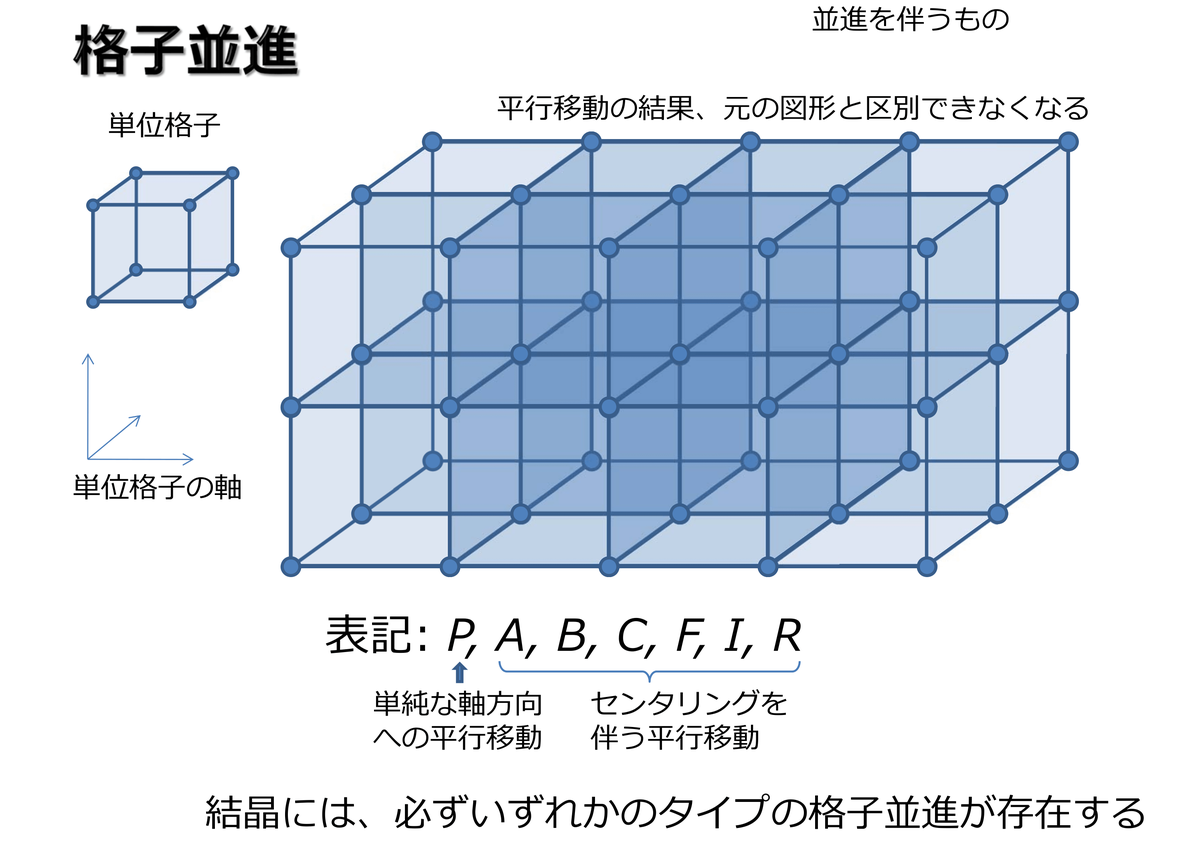
結晶系とブラベー格子の関係 PDF
空間充填によって構成された立体を空間充填立体(英:Space-filling polyhedron)と言い、空間充填によって埋め尽くされた空間を空間充填形という。定義からいえば空間はどんな空間でもよいが、単に空間充填・空間分割といえば、3次元ユークリッド空間の充填であることが多い。
空間充填 Space-filling Forvo Wikipedia Wikipedia
空間充填立体 Space-Filling Polyhedron Яндекс MathWorld
7:08
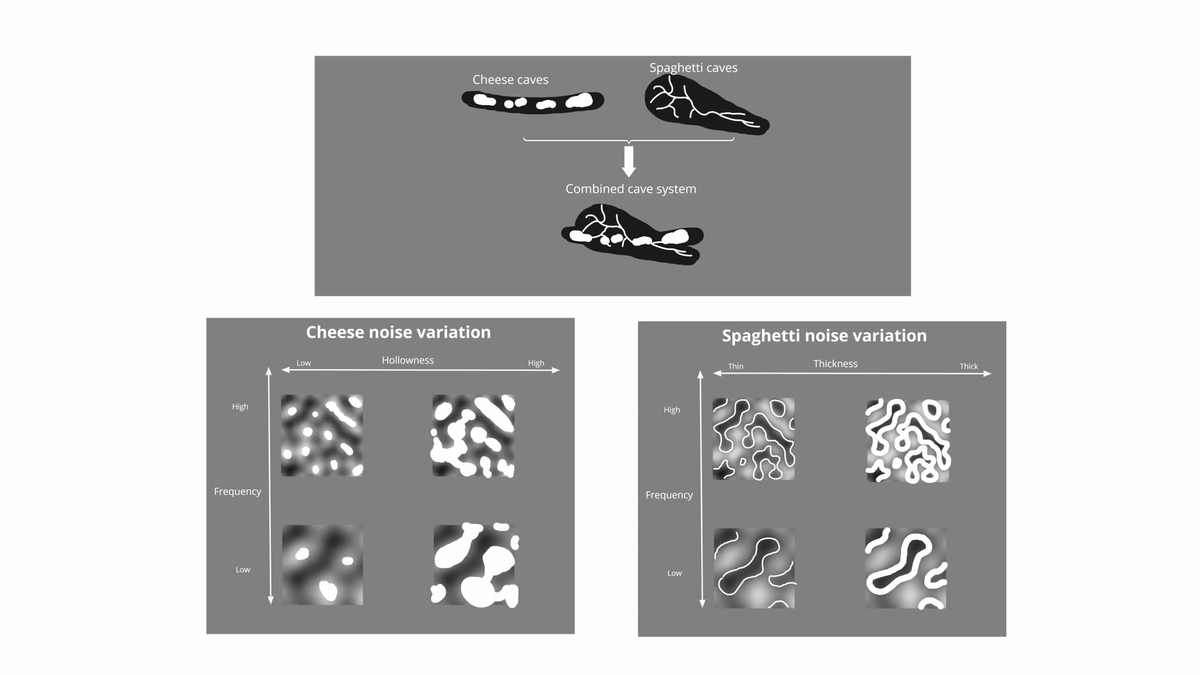
So a question that I get very often is what are spaghetti caves and cheese caves? And the best way to understand it is if you imagine an old television set with static noise black and white dots right.
And if you take those dots and you smoothen it out using a technique called purlin noise a mathematical technique and you decide that those white blobs are air and everything else is stone.
If you look at that, that becomes almost like a map of a cave system.
And that's kind of how we generate the caves.
And if you look at that picture those blobs look kind of like the holes in swiss cheese, at least we thought so, that's why we just call that cheese caves.
But we also want tunnels connecting them.
So in a similar way we can create another noise field right the black and white dots smudge it out using purlin noise and then we can decide that instead of white blobs being air and the rest being stone we decide that the border between white and black that thin ridge becomes air and the rest is stone.
And that gives us spaghetti-like caves.
So putting those together, cheese caves gives us these big kind of caverns, spaghetti caves gives us these connecting tunnels between them and then we add the old cave generation on top of that we get a ton of variation.
私がよく受ける質問は、「スパゲッティ・ケーブとチーズ・ケーブとは何か」というものです。これを理解する一番の方法は、古いテレビを想像してみてください。そこにはスタティックノイズと呼ばれる白黒の点があります。
それらの点を、パーリンノイズという数学的手法を用いて平滑化し、白い塊を空気、それ以外を石と決めてしまうのです。
これを見ると、洞窟システムの地図のようになります。
このようにして洞窟を生成しています。
この写真を見ると、これらの塊はスイス・チーズの穴のように見えますが、少なくとも私たちはそう考えました。
しかし、それらをつなぐトンネルも必要です。
同じように、黒と白の点をパーリンノイズでぼかして別のノイズフィールドを作り、白い塊が空気で残りが石になるのではなく、白と黒の境目の細い尾根が空気で残りが石になるように決めます。
そうすると、スパゲッティのような洞窟ができます。
これらを組み合わせると、チーズケーブでは大きな洞窟、スパゲッティケーブでは洞窟と洞窟の間をつなぐトンネル、さらに古い洞窟の世代を加えることで、膨大なバリエーションが生まれます。
9:00
This update has been kind of tricky because we're changing basically everything about how the world is generated in Minecraft.
But two of the main challenges especially for caves has been world height first of all.
We're making the world higher and lower so the y-coordinate starts at negative 64 instead of at zero and then extends too much higher than before and
that's hard because there's so much code that assumes a certain world height, we have to change so much code and do so much testing and fix so many bugs.
Plus performance, a bigger world means more stuff going on more stuff to load and that can slow things down, so that's one challenge.
The other challenges is water levels, we love local water levels they're really cool you get lakes and waterfalls.
But it's really tricky to deal with when these different water levels meet.
How do we avoid walls of water for example and things like that.
今回のアップデートは、『Minecraft』の世界の生成方法に関する基本的なすべてを変更することになるので、ちょっと難しいものでした。
しかし、特に洞窟の主な課題の2つは、まず世界の高さでした。
ワールドを高くしたり低くしたりしているので、Y座標はゼロではなくマイナス64から始まり、以前よりもはるかに高くなっています。
特定の世界の高さを前提としたコードがたくさんあるので、多くのコードを変更し、多くのテストを行い、非常に多くのバグを修正する必要があります。
また、パフォーマンスの面でも、世界が広くなると、それだけ多くのものを読み込むことになり、動作が遅くなる可能性があります。それは1つの課題です。
もうひとつの課題は、水位です。私たちは、湖や滝などのローカルな水位がとても好きです。
しかし、異なる水位が重なったときの処理は非常に厄介です。
例えば、水の壁をどうやって回避するかなどです。
パーリンノイズは、うまく使えばすごいことになります。
@Grabbus_Game Twitter
@phi6 Twitter
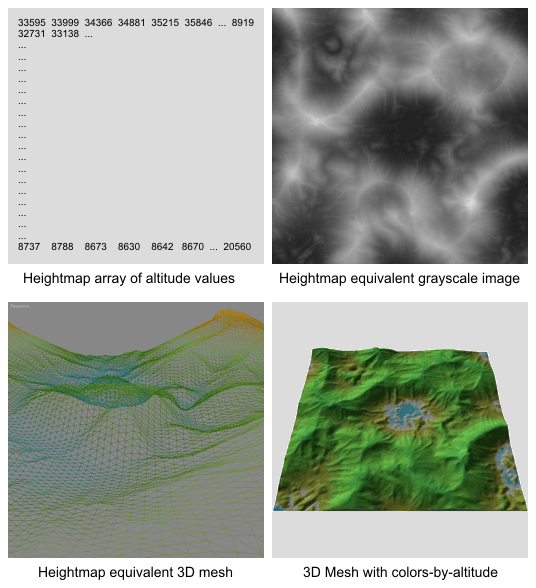
ハイトマップ配列の各値は、最終テレインメッシュオブジェクトの頂点の Z値 (高度) に直接対応します。ハイトマップを可視化するには、濃いグレーのピクセルが低高度、薄いグレーが高高度を表すグレースケールビットマップの使用をお勧めします。

Ken Perlin氏というコンピュータ科学教授が1983年に開発し、それから、多くのプログラムに使われているノイズ生成機能です。いくつかの引数(ファンクションの設定値)を設定することができ、変更することによって、波の形が変わります。引数を変更すると、波の特徴が変わります。
3Dの自動地形生成をやってみました! | SPLOUT BLOG
Ken Perlin Wikipedia
So i added some perlin noise to the missile battery (when fireing all at once). I think im satisfied for now.
そこで、ミサイルバッテリーにパーリンノイズを追加しました(一斉射撃時)。今のところ満足しています。
@AnkanX Twitter
2Dデータを3D都市モデルに変換します
Tom Kelly ResearchGate
都市道路 Urban Road
土地区画 Land Division
特徴量工学 Feature Engineering Wikipedia
@OskSta Twitter
2.1.1. Hierarchical structure
On the basis of land properties, forms, and transport links with the streets, the physical unit of a building lot can be defined in multiple scales. The hierarchy of block elements can be built consequently in the manner of “Block - Plot Series - Plot Sub-series - Physical Plots” and can be used to identify and analyze the spatial hierarchy of blocks.
階層構造
土地の特性や形状、道路交通網に基づいて、宅地という物理的な単位を複数のスケールで定義することができる。ブロック要素の階層は、結果的に「ブロック-区画系列-区画小系列-物理区画」の方法で構築することができ、ブロックの空間階層を識別し、分析するために使用することができる。
階層 Hierarchical hierarchy Forvo
交通網 Transport Link DMM
CityEngineは、都市の設計研究に携わる建築家、プランナー、関係者向けの生成ツールです(Esri CityEngine, 2020a)。
CityEngineシステムは、L-systemや拡張L-systemなど、複数の異なるツールで構成されています。次に、Müllerら(2006)は、コンピュータ生成アーキテクチャ(CGA)言語を構築する方法を拡張した(Smelikら、2014)。CGAは、建築物の手続き型モデリングのための新しい形状文法として、高い視覚的品質と幾何学的なディテールを持つ建築シェルを生成できる(Müllerら、2006年)。
L-system Яндекс Google MathWorld Wikipedia
Aristid Lindenmayer Wikipedia
そしてこの経験を基にBongfishは、社内にAIチームを立ち上げることになる。このチームは、さまざまな機械学習技術を使って、デザイナーがどのようにマップを構築するかを学習し、独自のAIが作成したマップを構築するシステムを作った。同チームは、マイクロソフトと連携する前にも、実際にいくつかのプロジェクトでこのシステムを使っている。

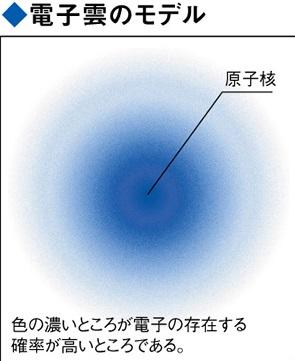
原子軌道 Atomic Orbital Wikipedia
本荘光史 researchmap

二重スリット実験 Double-slit experiment Яндекс コトバンク Wikipedia

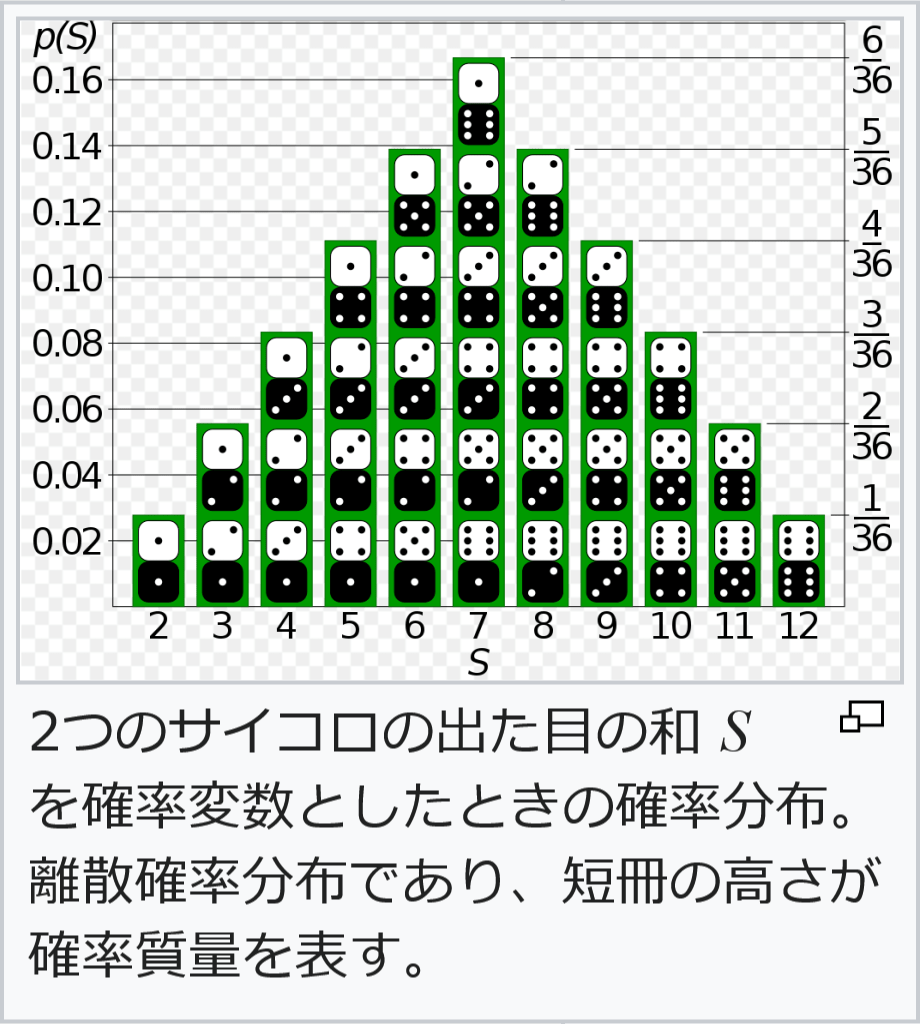
確率変数 コトバンク Random variable Forvo
確率分布 コトバンク Probability distribution Forvo
Allen Caldwell https://www.mpp.mpg.de/~lenz/course.html
MPP Wikipedia MPP

Andrius Velykis GitHub Hipparchus Core
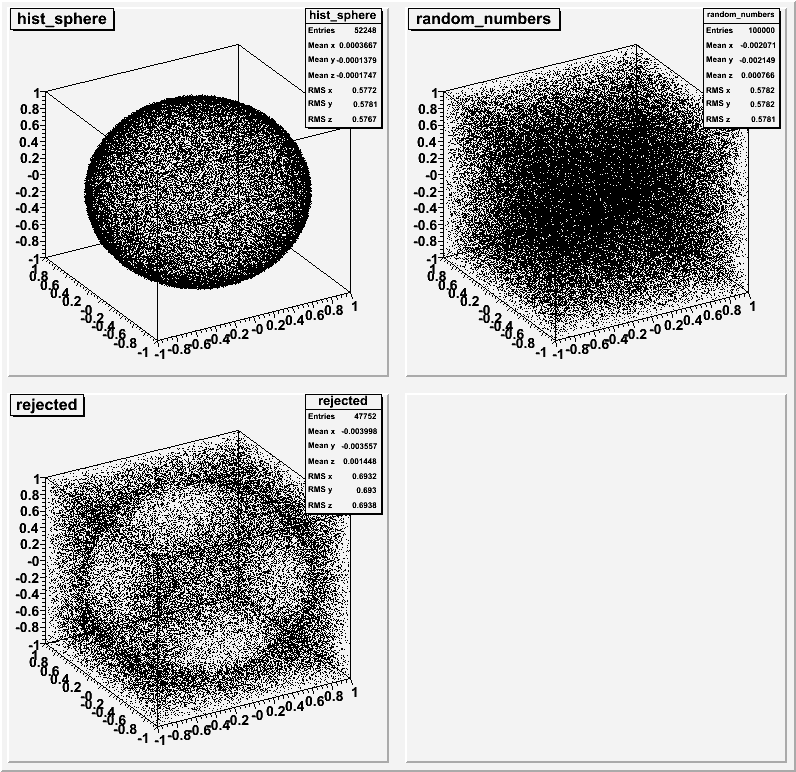
モンテカルロ法 GeoGebra
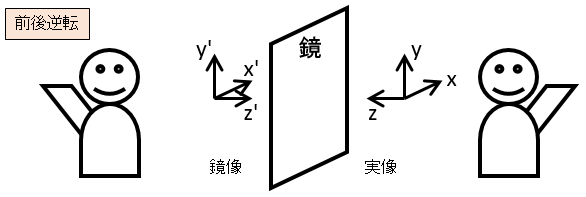
鏡の物理的機能は上で見たように鏡面の前後(z 軸)だけ反転し,鏡面の上下左右(x,y 軸)は反転しない
ここで注意が必要なのは z 軸は鏡面に垂直(法線ベクトル)であり,鏡の向きによって z 軸の向きも変わる
鏡のパラドックス

David Whyte Gizmodo
全体と部分の形状が相似の関係にあることを自己相似性を持つという。自己相似性を持つ図形は、全体の形状がその形状の各部分にも表れる、すなわち自分自身の縮小変換の集合で表せる。このような図形をフラクタルとよぶ。
| フラクタル | Fractal | Forvo | コトバンク | ||||
| 自己相似 | Self-Similarity | Forvo | コトバンク | Wikipedia | Wikipedia | ||
| 再帰 | Recursion | Forvo | コトバンク | Wikipedia | Wikipedia | ||
| 自己参照 | Self-Reference | Wikipedia | Wikipedia |
| ドロステ効果 | Droste Effect | Forvo | Wikipedia | |
| 合わせ鏡 | Wikipedia | Wikipedia |

| Sierpinski Gasket | Wikipedia | MathWorld | |||||
| コッホ曲線 | Koch Curve | Wikipedia | MathWorld | ||||
| フラクタル次元 | Fractal Dimension | Wikipedia | Wikipedia |
プログラミングの世界では、実行中のコードがそのコードの中で再び呼び出される処理のことを意味しており、たとえば「0に1を足してできた数(0+1)」を1に足す→「できた数(1+1)」を「先にできた数(0+1)」に足す」→「できた数(2+1)」を「先にできた数(1+1)」に足すという手順はフィボナッチ数列(0, 1, 1, 2, 3, 5, 8, 13…)と呼ばれる特殊な数列が生まれる処理としてよく知られています。
Sbbit
| 再帰 | Recursion | recursive | Forvo | IT用語辞典 | Wikipedia | MathWorld |
| 回帰 | Regression | regress | Forvo | コトバンク | MathWorld |
| Reddit |
Unity 3D Unreal Engine |
Electrical Engineering and Computer Science | MIT EECS | MIT OpenCourseWare
| MathWorld Wikipedia Wikipedia Wikipedia |
Mathematics Physics Shapes |
| Math | Diagrams | ||||||
| Math Solver | Microsoft | ||||||
| Visual Studio | Microsoft | VSCode | |||||
| DirectX | Microsoft | ||||||
| C# | Microsoft | SharpLab | |||||
| Python | Python | GitHub |
| @beesandbombs | @tdhooper | @jn3008 | |||
| @concinnus | @KangarooPhysics |
| Maxim Gumin | GitHub | ||||||
| 高橋啓治郎 | GitHub | Unity | |||||
| Christian Heinemann | GitHub | ALiEn | |||||
| Etienne Jacob | GitHub | ||||||
| miku | Zenn | ||||||
| SEGA | SlideShare | ||||||
| RWTH Aachen | GitHub | YouTube | |||||
| Károly Zsolnai | YouTube |